Floyd-Warshall 算法 Nov 11, 2020 算法 动态规划
Floyd-Warshall 算法使用一种不同的动态规划公式来解决所有结点对最短路径问题,运行时间为 Θ ( ∣ V ∣ 3 ) \Theta(|V|^3) Θ ( ∣ V ∣ 3 )
全源最短路径
Floyd 算法考虑的是一条最短路径上的中间结点 。
中间结点 :简单路径 p = < v 1 , v 2 , ⋯ , v l > p=<v_1,v_2,\cdots,v_l> p =< v 1 , v 2 , ⋯ , v l > p p p v 1 v_1 v 1 v l v_l v l { v 2 , v 3 ⋯ , v l − 1 } \{v_2,v_3\cdots,v_{l-1}\} { v 2 , v 3 ⋯ , v l − 1 }
假定图 G G G V = { 1 , 2 , ⋯ , n } V=\{1,2,\cdots,n\} V = { 1 , 2 , ⋯ , n } { 1 , 2 , ⋯ , k } \{1,2,\cdots,k\} { 1 , 2 , ⋯ , k } i , j ∈ V i,j\in V i , j ∈ V i i i j j j { 1 , 2 , ⋯ , k } \{1,2,\cdots,k\} { 1 , 2 , ⋯ , k } p p p p p p k k k p p p
如果 k k k p p p p p p { 1 , 2 , ⋯ , k − 1 } \{1,2,\cdots, k-1\} { 1 , 2 , ⋯ , k − 1 } i i i j j j { 1 , 2 , ⋯ , k − 1 } \{1,2,\cdots,k-1\} { 1 , 2 , ⋯ , k − 1 } i i i j j j { 1 , 2 , ⋯ , k } \{1,2,\cdots,k\} { 1 , 2 , ⋯ , k }
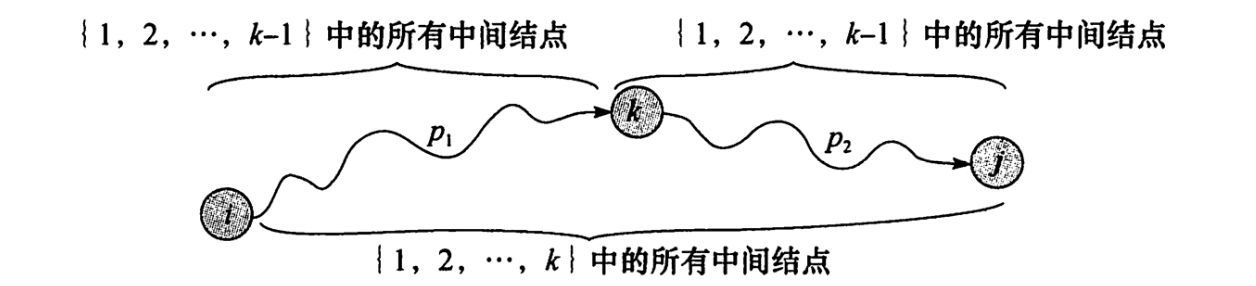
如果结点 k k k p p p p p p p 1 : i → k p_1:i\to k p 1 : i → k p 2 : k → j p_2: k\to j p 2 : k → j p 1 p_1 p 1 i i i k k k { 1 , 2 , ⋯ , k − 1 } \{1,2,\cdots, k-1\} { 1 , 2 , ⋯ , k − 1 } k k k p 2 p_2 p 2 k k k j j j { 1 , 2 , ⋯ , k − 1 } \{1,2,\cdots, k-1\} { 1 , 2 , ⋯ , k − 1 }
下图很好的展示了两种不同情况。
我们假设 d i j ( k ) d_{ij}^{(k)} d ij ( k ) i i i j j j { 1 , 2 , ⋯ , k } \{1,2,\cdots,k\} { 1 , 2 , ⋯ , k } k = 0 k=0 k = 0
此定义下,矩阵 D ( n ) = ( d i j ( n ) ) D^{(n)}=(d_{ij}^{(n)}) D ( n ) = ( d ij ( n ) )
我们可以自底向上计算最短路径权重,算法输入为 n × n n\times n n × n W W W D ( n ) D^{(n)} D ( n )
该算法包含三层 for 循环,运行时间为 Θ ( n 3 ) \Theta(n^3) Θ ( n 3 )
有向图的传递闭包
传递闭包
给定有向图 G = ( V , E ) G=(V,E) G = ( V , E ) V = { 1 , 2 , ⋯ , n } V=\{1,2,\cdots,n\} V = { 1 , 2 , ⋯ , n } i → j i\to j i → j G G G G ′ = ( V , E ′ ) G'=(V,E') G ′ = ( V , E ′ ) E ′ = { ( i , j ) } E'=\{(i,j)\} E ′ = {( i , j )} i i i j j j
思路
如果图 G G G i i i j j j { 1 , 2 , ⋯ , k } \{1,2,\cdots,k\} { 1 , 2 , ⋯ , k } t i j ( n ) = 1 t_{ij}^{(n)}=1 t ij ( n ) = 1 t i j ( n ) = 0 t_{ij}^{(n)}=0 t ij ( n ) = 0 ( i , j ) (i,j) ( i , j ) E ′ E' E ′ t i j ( n ) = 1 t_{ij}^{(n)}=1 t ij ( n ) = 1
t i j ( k ) = t i j ( k − 1 ) ∨ ( t i k ( k − 1 ) ∧ t k j ( k − 1 ) ) k ≥ 1 t_{ij}^{(k)}=t_{ij}^{(k-1)}\vee(t_{ik}^{(k-1)}\land t_{kj}^{(k-1)})\quad\quad k\geq 1 t ij ( k ) = t ij ( k − 1 ) ∨ ( t ik ( k − 1 ) ∧ t kj ( k − 1 ) ) k ≥ 1 我们同样使用递增的次序计算矩阵 T ( k ) = ( t i j ( k ) ) T^{(k)}=(t_{ij}^{(k)}) T ( k ) = ( t ij ( k ) )
此算法的时间复杂度仍然是 Θ ( n 3 ) \Theta(n^3) Θ ( n 3 )