对GAN的实验与思考

Sep 15, 2022
生成模型人工智能

GAN 的目标和行为的本质是什么？它的缺陷和改进方向又是什么？本文中笔者通过一些介绍，分析和实验来更加深入地探讨一下这个神奇的生成模型。

什么是生成模型？

什么是生成模型？以图片生成模型为例，我们可以将数据集中的真实图片视为一种服从某种概率分布的随机变量 $X$ 。同时，我们令模型生成得到的伪造图片为随机变量 $\hat{X}$ 。生成模型的目标是：使伪造图片的概率分布 $P(\hat{X})$ 和真实图片的概率分布 $P(X)$ 尽可能接近。

更直观地说，特定类型的图片（例如：人脸图片）一定满足一个先验的分布，但我们不知道，因此我们通过机器学习得到一个生成器（Generator， $G$ ）来接近这个分布。

但是，生成模型不仅如此。因为如果我们仅仅只是希望真假分布接近，模型直接把真实图片原封不动地吐出来不就好了吗？对于生成任务，我们自然会要求生成结果的多样性。然而在计算机中，模型的结构参数是确定的，因此相同的输入一定会得到相同的输出。在此情况下，如果我们要有多样的输出结果，我们的模型就一定要能够接受多样的输入。因此在任何生成模型中，一定要有一个随机噪声 $h$ 参与到模型的计算之中，来实现多样性。

我们假设生成模型 $G$ 的模型参数为 $\theta$ ，那么生成模型的数学表示为：

\hat{X}=G(\theta, h)

生成模型的目标是：

\min_{\theta} d(P(X), P(\hat{X}))

这里 $d(P_1, P_2)$ 代表的是两个概率分布之间的距离（差距）。“距离函数 $d$ 如何定义”是生成模型中最重要的问题之一。很多著名模型对此有探索：VAE 采用的是 KL 散度，经典 GAN 本质上采用的是 Jensen-Shannon 散度，WGAN 采用的是 Wasserstein 距离。怎样的度量公式才能更好地衡量两个具体的数据分布，是一个重要的话题。

什么是生成对抗网络？

生成对抗网络（Generative Adversarial Networks, GAN）是由 Goodfellow 提出的一种构思巧妙的数学模型，可以很好地完成生成任务。我们之前提到，生成模型的终极目标就是使 $\hat{X}$ 和 $X$ 更接近。不同于 VAE 模型显式地在损失函数中加入 KL 散度来实现，GAN 设计的初衷是通过一种对抗的方式来实现这一目标。

对抗的视角

GAN 由生成器 $G$ 和鉴别器 $D$ 组成。

$G$ 的目标是：根据输入的噪声 $h$ ，输出生成的 $\hat{X}$ 。

$D$ 的目标是：根据输入的 $X$ ，判断其来自于真实样本还是生成模型（二分类）。

通俗来讲， $G$ 不断地想生成更接近 $X$ 的 $\hat{X}$ 来混淆 $D$ 的判断，而 $D$ 也不断力图正确分辨输入的真假。在理想的对抗过程中， $G$ 和 $D$ 一同进步，直到最后 $D$ 无法分辨出 $G$ 生成的虚假 $\hat{X}$ 。我们用数学形式描述上述过程。首先，我们给出如下定义：

符号	意义
$P_{\mathrm{data}}$	真实样本的概率分布
$p_{\theta}$	生成样本的概率分布， $\theta$ 为模型参数
$p(h)$	随机噪声的概率分布，通常采用标准正态分布 $N(0,I)$
$X$	真实样本，来自 $P_{\mathrm{data}}$
$\hat{X}$	生成样本，来自 $p_{\theta}$

我们令真实样本为 1，生成样本为 0，因此 $D$ 希望 $D(X)$ 尽可能接近 1，希望 $D(\hat{X})$ ，也就是 $D(G(h))$ 更接近 0。将这个目标写成 log-likelihood 的形式如下：

V(D,G)=\mathrm{E}_{P_{\mathrm{data}}} \log D(X)+\mathrm{E}_{h\sim p(h)}\log(1-D(G(h)))

此处 $V(D,G)$ 代表着鉴别器 $D$ 的性能。那么 $D$ 的目标当然是最大化自己的性能，即：

\max_{D}V(D,G)

而 $G$ 的目标则是混淆 $D$ ，也就是最小化 $D$ 的性能。因此，GAN 的最终目标如下：

\min_{G}\max_{D} V(D, G)

这就是 GAN 的对抗过程。

数学的视角

即便上述过程听着很合理，它依然缺乏数学的支撑。在本节中我们将展示：GAN 对抗过程的本质就是在优化 $\hat{X}$ 和 $X$ 之间的 Jensen Shannon 散度。

最优鉴别器

在鉴别器优化阶段，根据公式 $\max_{D}V(D,G)$ ，我们可以在梯度为零处得到最优鉴别器 $D^*(X)$ ：

\begin{align} &\frac{\partial{V}}{\partial{D}}=0\\\ \to &\frac{P_{\mathrm{data}}(X)}{D(X)}-\frac{p_{\theta}(X)}{1-D(X)}=0\\\ \to &-p_{\theta}(X)D(X)+P_{\mathrm{data}}(X)-P_{\mathrm{data}}(X)D(X)=0\\\ \to &D^*(X)=\frac{P_{\mathrm{data}}(X)}{p_{\theta}(X)+P_{\mathrm{data}}(X)} \end{align}

Jensen-Shannon 散度

JS 散度是用来衡量两个分布的相似度的。它基于最常用的 KL 散度有两个重要优势：

JS 散度具有对称性，即 $\mathrm{JSD}(X_1||X_2)=\mathrm{JSD}(X_2||X_1)$
JS 散度取值范围是 $[0,1]$ ，是有限取值

因此，它也被称为是对称平滑版本的 KL 散度。我们这里写出 $P_{\mathrm{data}}$ 和 $p_{\theta}$ 的 JS 散度：

\begin{aligned} \mathrm{JSD}(P_{\mathrm{data}}\ ||\ p_{\theta})&=\mathrm{KL}(p_{\theta}\ ||\ p_{\mathrm{mix}})+\mathrm{KL}(P_{\mathrm{data}}\ ||\ p_{\mathrm{mix}})\\ \mathrm{where}\quad p_{\mathrm{mix}}&=\frac{P_{\mathrm{data}}+p_{\theta}}{2} \end{aligned}

GAN 的本质：优化 JS 散度

我们通过数学推导，可以得到 $\mathrm{JSD}(P_{\mathrm{data}}\ ||\ p_{\theta})$ 和 $V(D,G)$ 之间的关系。下面开始推导：

\begin{aligned} \mathrm{JSD}(P_{\mathrm{data}}\ ||\ p_{\theta}) & = \mathrm{KL}(p_{\theta}\ ||\ p_{\mathrm{mix}})+\mathrm{KL}(P_{\mathrm{data}}\ ||\ p_{\mathrm{mix}})\\ & = \sum_{X}\left[p_{\theta}(X)\log\frac{p_{\theta}(X)}{p_{\mathrm{mix}}(X)}+P_{\mathrm{data}}(X)\log\frac{P_{\mathrm{data}}(X)}{p_{\mathrm{mix}}(X)} \right]\\ & = -H(p_{\theta})-H(P_{\mathrm{data}})-\sum_{X}\left[\ p_{\theta}(X)\log p_{\mathrm{mix}}(X)+P_{\mathrm{data}}(X)\log p_{\mathrm{mix}}(X)\right] \end{aligned}

然后，我们将最优鉴别器 $D^*(X)$ 代入公式得：

\begin{aligned} \mathrm{JSD}(P_{\mathrm{data}}\ ||\ p_{\theta}) & = -H(p_{\theta})-H(P_{\mathrm{data}})-\sum_{X}\left[ p_{\theta}(X)\log\frac{p_{\theta}(X)}{2(1-D(X))}+P_{\mathrm{data}}(X)\log\frac{P_{\mathrm{data}}(X)}{2D(X)}\right]\\ & = -H(p_{\theta})-H(P_{\mathrm{data}})+H(p_{\theta})+H(P_{\mathrm{data}})+\sum_{X}\left[\ p_{\theta}(X)\log[2(1-D(X))]+P_{\mathrm{data}}(X)\log(2D(X))\right]\\ & = \sum_{X}\left[\ p_{\theta}(X)\log 2+P_{\mathrm{data}}(X)\log2\right]+\sum_{X}\left[\ p_{\theta}(X)\log(1-D(X))+P_{\mathrm{data}}(X)\log(D(X))\right]\\ & = 2\log 2 + V(D,G) \end{aligned}

因此，GAN 优化目标的本质实际上就是 JS 散度：

V(D,G)=\mathrm{JSD}(P_{\mathrm{data}}\ ||\ p_{\theta})-2\log 2

由此，我们从数学上证明了 GAN 模型设计的有效性。但是，由于 JS 散度的一些固有劣势以及一些工程问题，GAN 的训练过程往往很难达到理想状态（下文实验部分会具体论述）。

GAN 的结构

这里介绍一下我们用于实验的最基础的 GAN 结构。

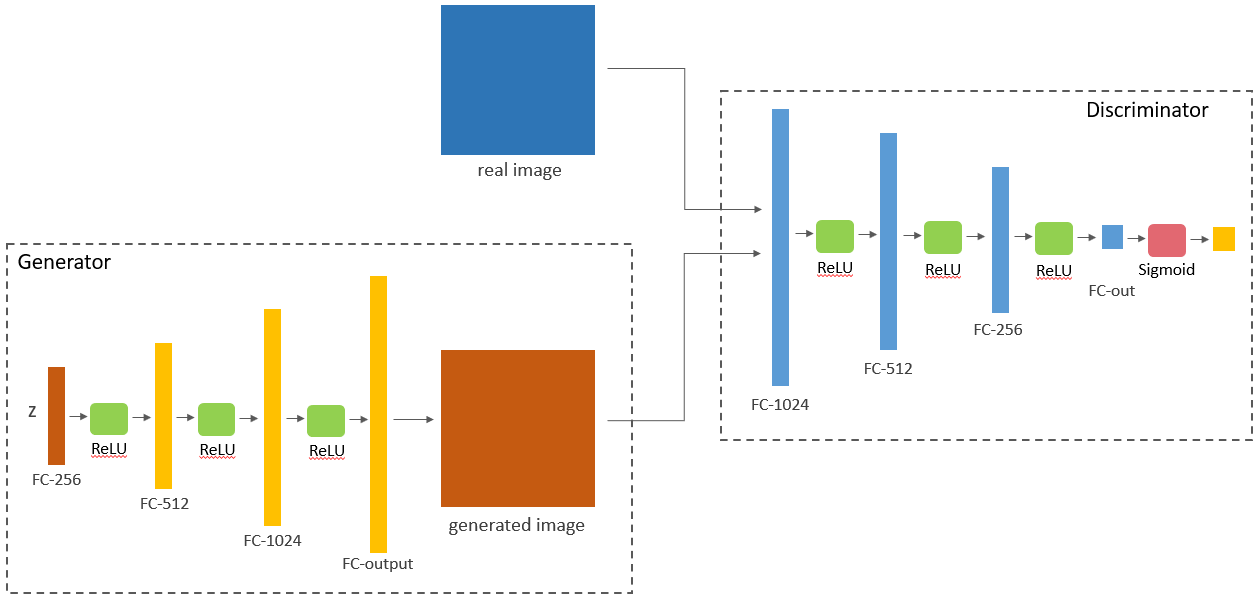
Vanilla GAN

Vanilla GAN，也就是最传统的 GAN，通过最简单的全连接层来实现生成器和判别器。其结构如下所示：

冷知识：Vanilla 原义为香草。因为香草味是冰淇淋最传统基本的口味，所以计算机领域常用 Vanilla 表示没有任何改变的，最传统的版本，例如 Vanilla GAN, Vanilla VAE。

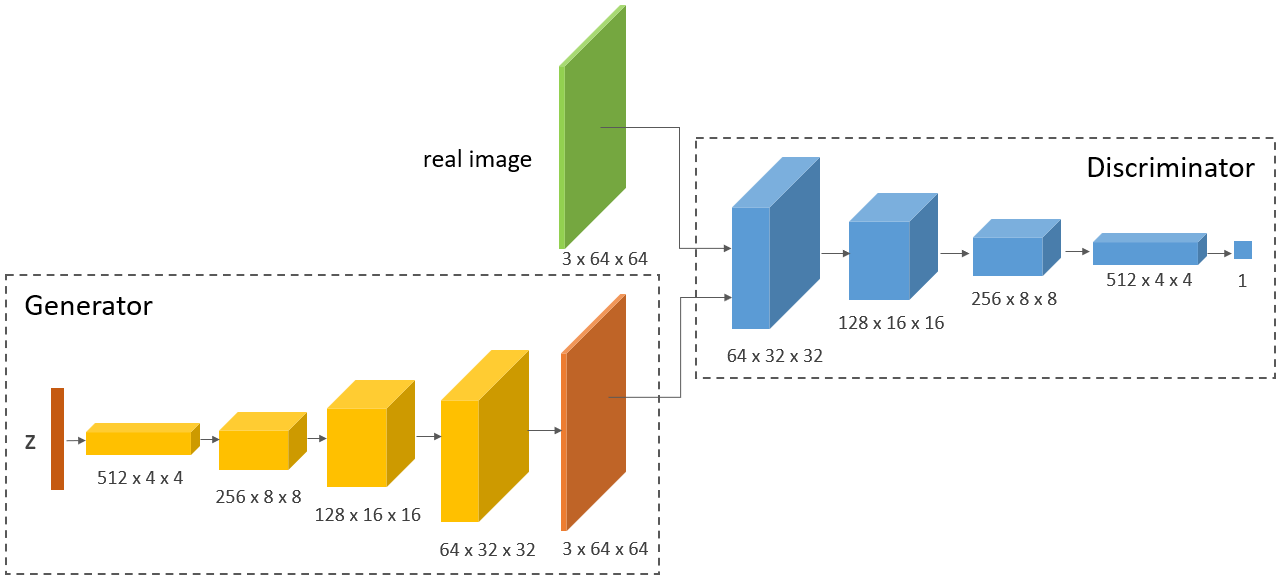
DCGAN

DCGAN 在传统 GAN 的思想上，用更强力的卷积层代替了 Vanilla GAN 的全连接层。其结构如下（此处用 $64\times 64$ 图片为例）：

生成结果

我在 CelebA 人脸数据集和 CUB200_2011 鸟类数据集上测试了 DCGAN 的生成能力，我们一起来看一下生成结果。

由于算力有限，算法性能不是我们关注的重点，生成的结果虽有明显瑕疵，但不影响我们的学习实验。

实验：训练中的对抗平衡

定性分析

GAN 采用的是一种对抗式训练，对抗的双方（鉴别器和生成器）是否“势均力敌”直接影响生成性能的好坏。

实验主要通过调整鉴别器学习率 $lr_{D}$ 和生成器学习率 $lr_{G}$ 来实现。首先，我设置了相同的学习率 $lr_{D}=lr_{G}=1\times 10^{-4}$ ，并绘制了 $D$ 和 $G$ 损失函数的曲线（下图最左）。我们可以观察得到，在第10轮左右，鉴别器的损失函数几乎归零，发生梯度消失的现象，导致生成器的损失值开始明显上升。

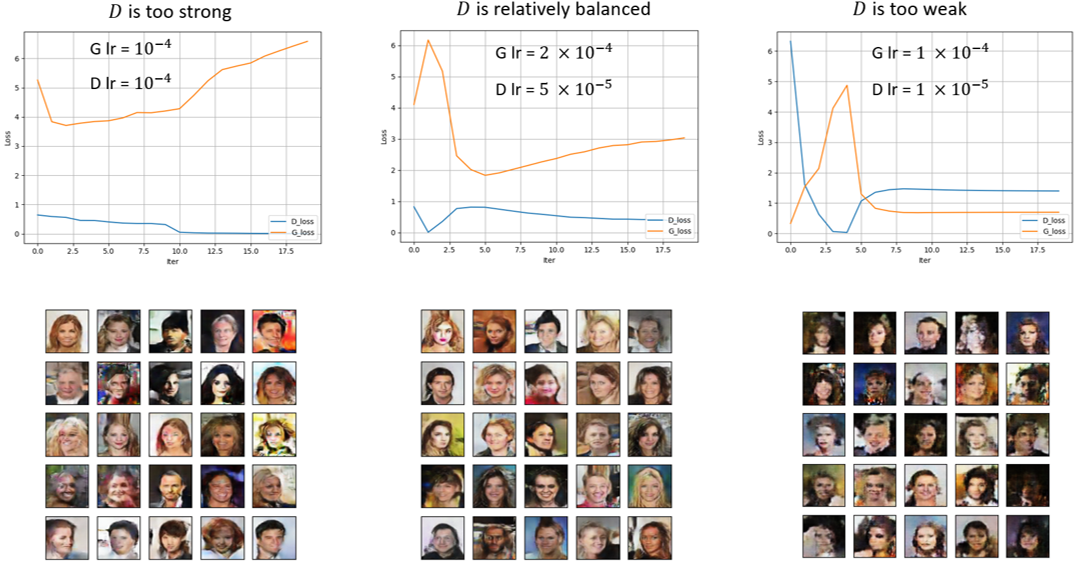
由此现象，我们可以归纳出以下两点：

鉴别器损失归零，直观上来说代表鉴别器已经完全将真图和假图区分开来，生成器已经无法欺骗鉴别器了。这就说明，如果鉴别器训练太快会导致生成器无法同步进步，导致梯度消失，生成器无法学到有用的信息。
此外，因为我们在相同的训练设置下得到了不平衡的训练结果，这说明分类任务和生成任务的复杂程度是有较大差异的，这种难度差异就是GAN训练困难的本质原因。

因此，我们改变学习率设置，得到了多组实验结果和曲线。我们可以发现，在 $lr_{D}=5\times 10^{-5}$ 和 $lr_{G}=2\times 10^{-4}$ 时生成的结果较好，同时损失函数曲线（上图中间）也呈现出较好的对抗性质。而当我们进一步减少 $lr_{D}$ ，我们发现鉴别器损失收敛于高位，同样无法进步。

定量分析：理想状态是什么？

与此同时，我也想构想一下理想状态下的曲线是什么样的。回到我们之前得到的最有情况下鉴别器的公式：

D^*(X)=\frac{P_{\mathrm{data}}(X)}{p_{\theta}(X)+P_{\mathrm{data}}(X)}

在实验中，我们每次给鉴别器相同数量的真图和假图，因此在GAN理想收敛时， $D$ 应该永远返回0.5，代表鉴别器完全无法区分真假。此时，鉴别器的损失函数值应为：

\mathrm{BCE}=-\frac{1}{2n}\left[\sum_{i}^n \left(-\ln \frac{1}{2}-0\right)+\sum_{i}^{n}\left(-0-\ln\frac{1}{2}\right)\right]=-\ln\frac{1}{2}\approx 0.6931

因此，理想的损失函数曲线中，鉴别器应该大致收敛于0.69左右的位置。在理论支撑下，我尝试了更多的学习率，但是始终没有调出理想的鉴别器曲线（见下图）。

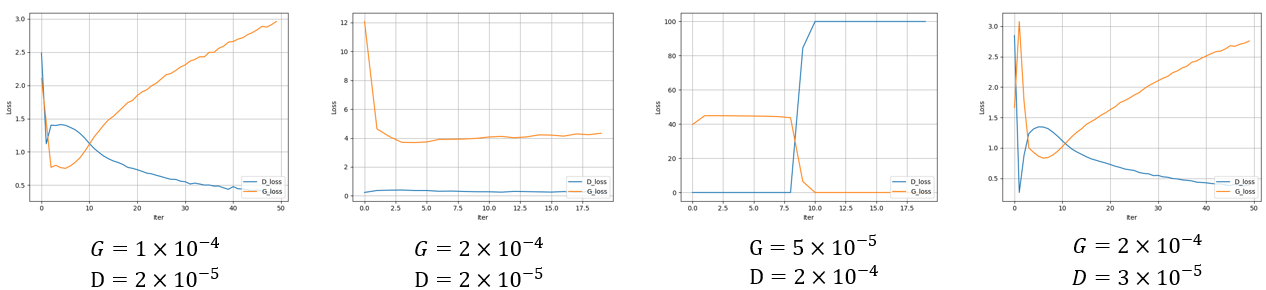
可能要保持 $G$ 和 $D$ 在整个训练过程中平衡几乎是不可能完成的任务。对于某一特定任务的调参尚且如此困难，这让我明白，GAN的改进仅用调参来优化是乏力低效的，必须从理论层面进行突破。不只是GAN，机器学习的研究皆是如此。

我们必须面对最重要的那个问题，否则我们将被无数琐碎的小问题缠身。

特征可视化：眼见为实

鉴别器失效

理论上在 GAN 的训练下，最终鉴别器将完全无法区分图片的真假，那么事实是否真的如此呢？我们本节利用 PCA 和 t-SNE 技术来可视化鉴别器的行为，以验证这一结论。

我们采用对比实验，首先我们使用一个训练较好的 GAN 的鉴别器，输入256张来自真实数据集的图片和256张由生成器生成的图片。对于鉴别器的每一层卷积层，我们提取其输出特征，用 PCA 和 t-SNE 降至三维进行可视化，如图所示。

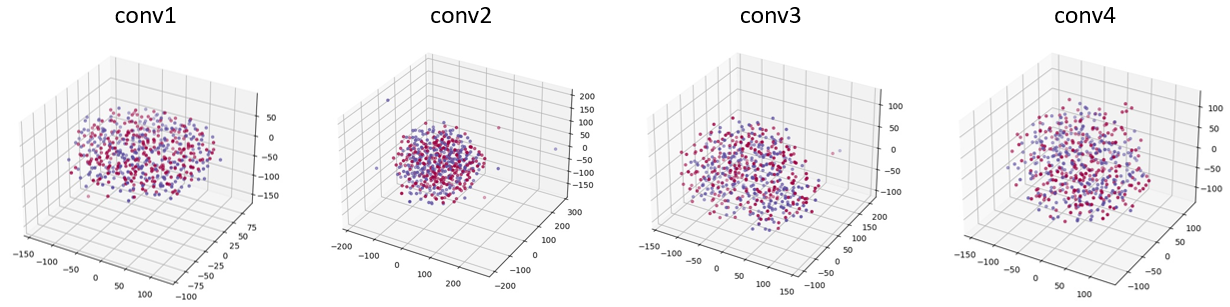
观察可得，真实图片（红点）和生成图片（蓝点）完全没有区分开混作一团，这为鉴别器无法区分真假图片提供了有力支撑。

同时，我们使用我们之前训练失败的GAN进行同样的实验（这个GAN的鉴别器训练超前于生成器），得到如下图所示的结果。

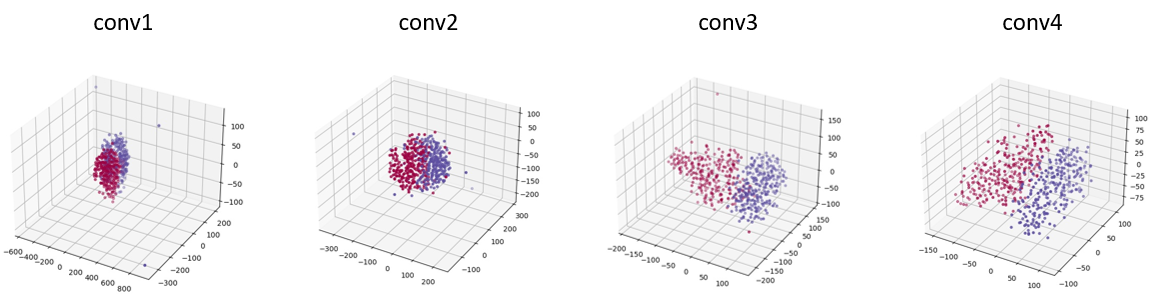
观察可得，正负样本在图中被很好的区分开了，这证明了在鉴别器训练超前的失败案例中，鉴别器能够很好区分真假图片。

因此，在理想状态下，GAN的鉴别器应该无法区分真假才合理。

隐变量分析

隐空间和图像域的连续性

本实验中，我们随机从正态分布中采样两个隐藏变量（10维），分别作为开始值 $h_{\mathrm{start}}$ 和结束值 $h_{\mathrm{end}}$ 。我在二者之间均匀取100个插值输入 $G$ 生成对应图片。我们一共进行了三组实验，如下图所示。

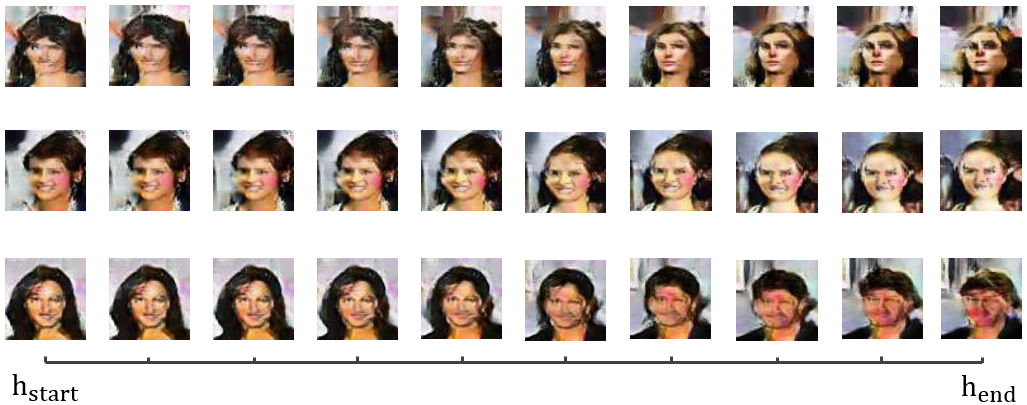
我们可以观察到：隐变量的连续变化引起了生成图片的连续变化，说明隐空间到生成图像域是一种连续映射（continuous mapping）。

维度是否承载语义信息

在这个实验中，我们随机采样初始隐变量，改变其中一个维度在 $[-2,2]$ 之间均匀变化，由此来看每个维度是否决定图片的某些特性。实验结果如下图，其中每一维度我们只展示了 $-2, -0.7, 0.7, 2$ 对应的结果。

从结果可知，虽然我们可以发现某些维度的改变引起了生成图片的一些语义的变化，如性别，发型，肤色，姿态等，但是并没有表现出明显的语义特征。想要维度单独控制特定语义特征，我们需要能够解耦维度的GAN技术。

隐变量语义加法

我经常看待对GAN隐变量的加减操作后生成的图片呈现神奇的语义特征，因此我也想尝试。在本实验中，我首先取了微笑的人脸图片对应的隐变量 $h_1$ 以及一些无表情人脸图片对应的隐变量 $h_2$ ，将 $h=h_1+h_2$ 进行生成，得到的实验结果如下所示。

观察可得， $h$ 生成的图片保留了 $h_1$ 包含的微笑特征和 $h_2$ 包含的姿态特征（正视 or 侧视），一定程度上体现了隐变量包含着丰富的语义信息。

如何评估生成器能力？

机器学习中，分类模型的评估可以简单地通过和 ground truth 比较得到准确率。然而，生成模型由于缺少 ground truth，因此难以直观地进行评价。一种最为直观的方法是比较生成图片分布和真实图片分布的相似度，这也是目前最主流的评价方法之一：FID score。

Frechet Inception Distance

Frechet Inception Distance (FID) 通过计算真实图片和生成图片之间分布的距离评估生成模型性能，越低越好。它采用预训练好的 Inception v3 模型将每张图片提取为 2048 维的特征向量，再通过下式计算二者的距离 $d$ ：

d^2=\lVert\mu_1-\mu_2\rVert^2+\mathrm{Tr}\left(C_1+C_2+2\sqrt{C_1C_2}\right)

其中， $\mu_1$ 和 $\mu_2$ 对应真图和假图特征向量的均值， $C_1$ 和 $C_2$ 对应二者的协方差矩阵， $\mathrm{Tr}$ 是矩阵的迹（矩阵主对角线元素和）。

我也用 FID score 来验证了下我的生成模型在每一轮的性能，如下图所示。实验方法是每一轮让模型生成100张图片，进行 FID score 的计算。

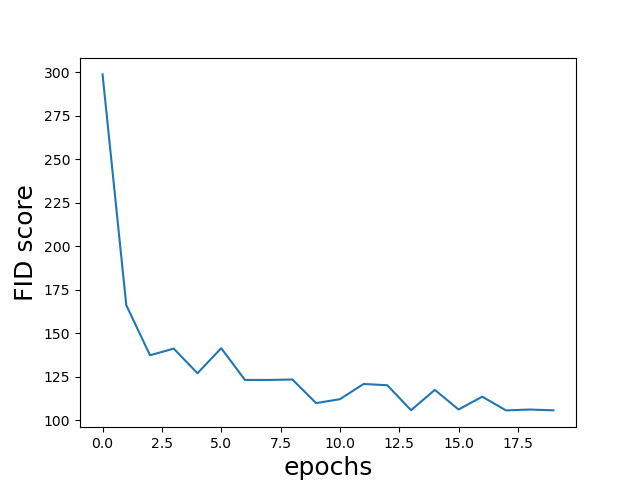
可以看到，我们的模型在训练过程中，性能确实呈现变好的趋势。

小结

这篇博客也暂时告一段落了。这是我最深入的一次对生成对抗网络的研究和学习，从理论和实践层面，获得了更加深刻的理解。但是，仍然有很多的实验和理论没有穷尽，比如 WGAN 如何简化训练？隐变量各个维度如何解耦？如何加入条件信息？也有很多未验证的假设和实验，需要时间和灵感去一个个实现。

期待下次与GAN相会时，我们都已迎来新的蜕变。

参考文献

[1] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv e-prints, page arXiv:1511.06434, November 2015.

[2] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. arXiv e-prints, page arXiv:1706.08500, June 2017.

[3] Martin Arjovsky and Léon Bottou. Towards Principled Methods for Training Generative Adversarial Networks. arXiv e-prints, page arXiv:1701.04862, January 2017.

[4] Martin Arjovsky, Soumith Chintala, and Léon Bottou. Wasserstein GAN.arXiv e-prints, page arXiv:1701.07875, January 2017