生成模型

Feb 15, 2021
生成模型人工智能

今天，我们来谈一谈生成模型。

无监督学习即训练数据无标签，也就是说生成模型解决的是无监督学习中密度估计的问题。在生成模型的世界中，我们可以将任何观测到的数据，记为数据集 $\mathcal{D}$ ，视为一个在概率 $p_{data}$ 上的有限采样集。所有生成模型的最终目标就是：给到生成模型观测的数据 $\mathcal{D}$ ，能够估计概率分布 $p_{data}$ 。

换句话说，我们从分布 $p_{data}(x)$ 中采样一个数据集 $D$ ，生成模型会学习到一个模拟这一分布的概率分布 $p_{model}(x)$ ，生成模型的目标是使得 $p_{data}(x)$ 和 $p_{model}(x)$ 尽可能相似。

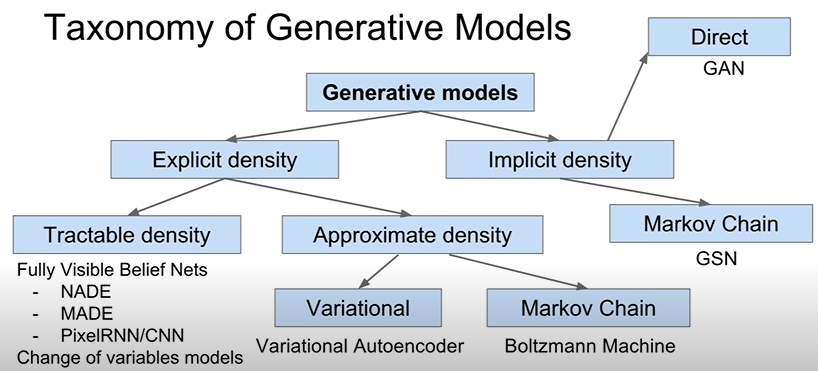
生成模型分类

Pixel

全可见置信网络

显式密度模型：我们可以用链式法则来将完整图片的概率分解成一维的分布：

p(x)=\prod_{i=1}^{n}p(x_i|x_1,\cdots,x_{i-1})

其中 $p(x)$ 是整个图片的概率， $p(x_i|x_1,\cdots,x_{i-1})$ 在给定所有其他像素时，第 $i$ 个像素值的概率。因此，我们需要将图片的像素排序 $i,\cdots,i$ 。不同的先序依赖关系就得到了不同的实现方式。

PixelRNN

在 PixelRNN 中，我们从左上角开始生成图片像素，使用 RNN（LSTM）来决定和前序像素的依赖关系。像素的生成循序如下所示：

PixelCNN

在 PixelCNN 中，我们同样从左上角像素开始生成，当前像素依赖于前序一块区域内的所有像素，并通过 CNN 进行实现，如图：

以上两者的训练目标都是最大化训练图像的概率。

PixelRNN/CNN 的优势在于：

可以显式地计算图片 $p(x)$
这种显式的训练数据概率给出了很好的评估度测度
可以很好地采样

他们的劣势就是必须串行地生成，这是十分低效的。

变分自编码器

变分自编码器（Variational Autoencoder, VAE）中，我们定义一个关于隐变量 $z$ 的可解密度方程：

p_{\theta}(x)=\int p_{\theta}(z)p_{\theta}(x|z) \mathrm{d} z

自编码器

自编码器（Autoencoder，AE）可以理解为用一种无监督的方法，从无标签训练数据中，学习一个低维的特征表示。假设输入数据为 $x$ ，自编码器将它编码为一个更低维度的特征向量 $z$ 。 $z$ 中往往包括了 $x$ 中最重要的特征维度。通过解码器，我们可以从 $z$ 恢复出一个输出向量 $\hat{x}$ 。

在训练自编码器的过程中，我们希望解码得到的 $\hat{x}$ 和原来的 $x$ 尽可能相似，因此我们设置损失函数为 L2 损失函数：

\mathcal{L}=||x-\hat{x}||^2

变分自编码器

对于数据概率：

p_{\theta}(x)=\int p_{\theta}(z)p_{\theta}(x|z)\mathrm{d}z

其中 $p_{\theta}(z)$ 可以视为简单的高斯先验分布，同时 $p_{\theta}(x|z)$ 也可以从解码器的神经网络中得到的，但是积分这个操作是难以优化的。

对于后验密度：

p_{\theta}(z|x)=p_{\theta}(x|z)p_{\theta}(z)/p_{\theta}(x)

其中 $p_{\theta}(x)$ 同样难以得到，因此我们无法直接优化概率公式。

一个解决方法是：定义一个额外的编码器 $q_{\phi}(z|x)$ 来近似 $p_{\theta}(z|x)$ 。这样，我们可以得到关于数据概率的一个下界，并且它是可解、可优化的。

因为生成器中，编码器和解码器都是有概率性质的，而任何一个概率都有均值和协方差。因此，我们可以根据编码器和解码器的均值和协方差，创造一个 $p\sim \mathcal{N}(\mu, \sum)$ 的高斯分布进行采样。

有了上述编码和解码网络，我们可以计算出数据概率：

\begin{aligned} \log p_{\theta}(x^{(j)}) &=E_{z\sim q_{\phi}} \left[\log p_{\theta}(x^{(i)})\right]\\ &=E_{z}\left[\log \frac{p_{\theta}(x^{(i)}|z)p_{\theta}(z)}{p_{\theta}(z|x^{(i)})}\right]\\ &=E_{z}\left[\log \frac{p_{\theta}(x^{(i)}|z)p_{\theta}(z)}{p_{\theta}(z|x^{(i)})}\frac{q_{\phi}(z|x^{(i)})}{q_{\phi}(z|x^{(i)})} \right]\\ &=E_{z}\left[\log p_{\theta}(x^{(i)}|z)\right]-E_{z}\left[\log\frac{q_{\phi}(z|x^{(i)})}{p_{\theta}(z)}\right]+E_{z}\left[\log\frac{q_{\phi}(z|x^{(i)})}{p_{\theta}(z|x^{(i)})}\right]\\ &=E_z\left[\log p_{\theta}(x^{(i)}|z)\right]-D_{KL}(q_{\phi}(z|x^{(i})||p_{\theta}(z))+D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)})) \end{aligned}

第一项可以通过采样近似得到，第二项（KL散度）有很好的闭式解。第三项虽然难解，但是可以肯定它是非负的，因此第一第二项可以组成一个目标函数的下界，并且它是可优化的。我们定义如下新损失函数：

\mathcal{L}(x^{(i)},\theta,\phi)=E_z\left[\log p_{\theta}(x^{(i)}|z)\right]-D_{KL}(q_{\phi}(z|x^{(i})||p_{\theta}(z))

我们有下界关系：

\log p_{\theta}(x^{(i)})\geq \mathcal{L}(x^{(i)},\theta,\phi)

我们的优化过程就是最大化下界：

\theta^*,\phi^*=\arg\max_{\theta,\phi}\sum_{i=1}^{N}\mathcal{L}(x^{(i)},\theta,\phi)

VAE 的优势在于

是生成模型的一种有原则的实现方法
允许来自 $q(z|x)$ 的干扰，是一种有用的特征表示方法。

VAE 的劣势在于

最大化概率的下界是一种间接的评价方法，没有 PixelRNN/CNN 的评价来得直接
和 GAN 相比，VAE 的采样质量更加模糊低劣

生成对抗网络

生成对抗网络（Generative Adversarial Networks，GAN）不再使用一个显式的密度函数，而是使用博弈论中一种双方对抗的方式，学习生成。生成模型的问题在于，我们无法直接从复杂高维的训练分布中进行采样。GAN 提供的方法是从简单分布（如随机噪声）中进行采样，然后学习一种将采样变成训练分布的转换器。这个转换器会比较复杂，因此我们使用神经网络来表示它。

训练：双人游戏

生成网络：生成逼真的图片来愚弄鉴别网络

鉴别网络：分辨真实的图片和虚假生成的图片

该训练过程的目标函数为：

\min_{\theta_g}\max_{\theta_d}\left[E_{x\sim p_{data}}\log D_{\theta_d}(x)+E_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z)))\right]

鉴别网络的输出值为 0~1，代表图片的真实程度。其中 $D_{\theta_d}(x)$ 是鉴别网络对真实图片的输出值， $D_{\theta_d}(G_{\theta_g}(z))$ 是鉴别网络对生成图片的输出值。

我们也可以分别写成两个式子：

鉴别器梯度上升：
$\max_{\theta_d}\left[E_{x\sim p_{data}}\log D_{\theta_d}(x)+E_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z)))\right]$
生成器梯度下降：
$\min_{\theta_g}E_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z)))$
但是， $\log(1-D_{\theta_d}(G_{\theta_g}(z)))$ 的函数图像，在采样初期（大部分采样为假）时梯度很小，不利于生成器更新，而在采样后期（大部分采样为真）的时候反而梯度很大，这使得整体性能不佳。因此，我们将生成器的目标函数稍加改动：
$\max_{\theta_g}E_{z\sim p(z)}\log(D_{\theta_d}(G_{\theta_g}(z)))$
也就是将 “使鉴别器鉴定正确的概率最小化” 变成 “使鉴别器鉴定错误的概率最大化”，这个改动没有改变整体的优化目标，却使得目标函数的梯度由大到小变化，但是在实践中性能大大增强。

伪代码

可解释向量操作

事实上，噪音向量 $z$ 的数学操作在一定程度上是可解释的。例如一个人像生成网络可以有如下操作：

解释一下，如果我们通过噪音向量 A 组生成的都是“微笑女性”的图片，噪音向量 B 组生成的都是“中性女性”的图片，噪音向量 C 组生成的都是“中性男性”的图片，那么我们可以通过 D=A-B+C 获得生成“微笑男性”的噪音向量组 D。这也正是因为噪音向量 $z$ 中不同维度和生成图片特征相对应导致的。

GAN 不用显式的密度函数，而是用博弈论方法在双方博弈中训练分布，有很好的采样结果。

GAN的劣势在于：

充满技巧性，训练更加不稳定
不能处理推断查询（inference queries），例如 $p(x)$ 和 $p(z|x)$

GAN 的热点研究方向有：

更好的损失函数设计，更稳定的训练（Wasserstein GAN, LSGAN…）
Conditional GANs, GANs 的各种应用

以下是一些相关的资源。

Pix2pix: https://phillipi.github.io/pix2pix/

Gan Zoo: https://github.com/hindupuravinash/the-gan-zoo

tips & tricks for training GANs: https://github.com/soumith/ganhacks

总结

以上是生成模型介绍以及三种最流行的生成模型的简介，图片信息来源于斯坦福大学公开课：

课程链接：https://www.youtube.com/watch?v=5WoItGTWV54